Ученые давно ломают головы как доступно и интересно рассказать подрастающему поколению о математических законах. Очередную попытку в этом направлении предпринял Яндекс и Международное общество исследователей в области психологии математического образования. На конференцию в Москве "Психология и технологии в математическом образовании" они собрали ученых из 16 стран мира.
Начнём с мозга
| Мари Арсалиду |
На протяжении последних 20 лет считалось, что только теменные и затылочные области ответственны за выполнение математических операций, - следует из доклада доцента департамента психологии НИУ ВШЭ Мари Арсалиду. - Однако благодаря развитию компьютерной томографии выяснилось, что при выполнении некоторых задач задействуются префронтальные области, которые ученые до этого связывали с эмоциональными переживаниями. В частности, существует так называемая островковая доля, которая отвечает за голод и жажду, и небольшая ее часть активизируется при выполнении некоторых математических операций. Эта область также реагирует на обещанное вознаграждение, необходимость сосредоточиться и вынести суждение.
Исследование показывает, что во время изучения математики ребенок тренирует когнитивные функции, используемые в повседневной жизни, и при этом математический неуспех в школе может быть вызван тем, что ребенок в дошкольном возрасте недостаточно времени уделял какому-либо виду деятельности, например, объятиям с матерью или игре в песочнице. Исследование пока не завершено, поэтому точные взаимосвязи еще только предстоит установить.
За сложными психологическими терминами и исследованиями понятно одно: мотивация существует на физиологическом уровне в островковой доле, и она играет огромную роль в решении математических задач, поэтому ребенка нужно мотивировать и вознаграждать за успехи, а не ругать за непонимание.
Движение - это знания
Раньше считалось, что в начальной школе нужно перевести ребенка с уровня предметного мышления на уровень абстрактного. Учиться надо, сидя за столом в удобной позе, на протяжении длительного периода времени. Сегодня подход меняется.
Обучение - это постоянное движение в пространстве, - убежден Дор Абрахамсон, нейроученый, исследователь и профессор факультета педагогики в Калифорнийском университете.
 |
| Дор Абрахамсон |
Психологи давно пришли к выводу, что в развитии ребенка и подростка на первом месте стоит опыт, а знания — на втором, вот только перенести этот тезис на математическое образования до сих пор никто не решался. Тут во главе угла теория.
Абрахамсон использует сенсорные экраны, чтобы объяснять ученикам начальной школы такие понятия, как дроби и пропорции. Например, прямоугольник 1х3 нужно пальцами растянуть до прямоугольника 3х9, сохранив пропорции. Так дети легко понимают одну их самых сложных тем начальной школы: почему 13= 39. Ключ к пониманию, по мнению ученого, заключается в том, что это явление теперь можно “потрогать”.
Но если в начальной школе "обучение на пальцах" использовалось давно, то в средней и старшей школе математика на 100 процентов переведена в абстрактную плоскость. Вы только попробуйте "потрогать" синус или "схватить" биссектрису. А ведь именно этим сегодня занимаются психологи, пытаясь перевести математику обратно на понятный для детей и подростков уровень, где все можно пережить и потрогать.
 |
| Анна Шварц |
Группа ученых, в которой участвует Анна Шварц исследователь из Института математического и научного образования им. Г. Фройденталя, старший научный сотрудник МГУ и методист проекта "Яндекс.Учебник", также разрабатывает способы объяснения с использованием больших сенсорных панелей.
К примеру, одной из тем, которая уже эффективно преподается с помощью сенсорных панелей, стала парабола. Двигая график, восьмиклассники видят, как меняются значения x и y, и то, что парабола — не просто изогнутая линия, а кривая, оба конца которой уходят в бесконечность.
Разница с обычными уроками в том, что ученику нужно обеими руками коснуться огромного треугольника на экране и произвести с ним действие. Задействуется мышечная память, математика становится частью телесного опыта.
Знания у детей, которые задействуют тело при обучении, можно сравнить с умением кататься на велосипеде: если один раз научился, то не разучишься за всю жизнь. Ведь, когда человек двигается в процессе запоминания, то задействуются моторные навыки, как если бы ребенок действительно учился кататься на велосипеде или на коньках.
В шутке сила
Не использовать тренды современной жизни в обучении было бы неправильным, а потому новый необычный способ преподавать математику предложила Орнелла Робутти из Туринского университета. Она заметила, что математические мемы в социальных сетях мотивируют школьников и студентов к изучению предмета. Мем — это шутка, и, если школьник ее не понимает, то он ищет в интернете информацию, чтобы понять ее. Когда шутка построена на математическом знании, дети с удовольствием изучают математику, обсуждают ее и смеются.

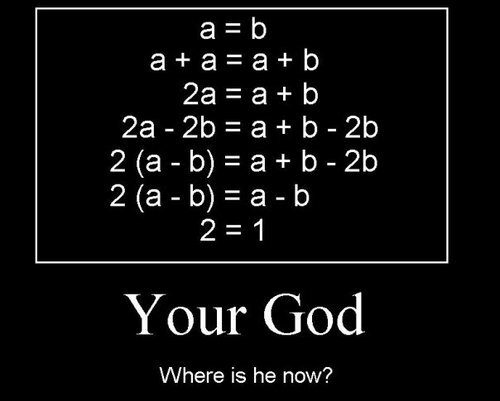
Вспомните классическое: "Пифагоровы штаны во все стороны равны",- это ведь тоже мем, но доинтернетовской эпохи. Сколько школьников советского времени пыталось объяснить это высказывание...
Современные ученые пошли дальше: проводили контрольные в виде мемов, поручали детям придумывать математические мемы, вывешивали математические мемы в общественных местах,- результат не заставил себя ждать. Дети заинтересовались математикой и стали активно участвовать в "шутливом" образовании, ведь цифры и формулы вдруг превратились в шутку, анекдот, понятный лишь разбирающимся… А смех и хорошие эмоции - это лучший цемент для знаний...
Конечно, одной конференции мало, чтобы понять, как проще преподавать математику,- пока ученые лишь поделились результатами исследований и наметили пути, которыми стоит воспользоваться и простым учителям. Во всех новых исследованиях математика связывает области мозга, отвечающие за абстрактные вычисления, с областями, задействованными в других операциях: эмоциях, движениях, ощущениях. Вот и получается, что нужно делать обучение интересным, интерактивным и максимально мобильным, чтобы “включались” все отделы мозга ребенка. Только так математика из скучного и “ненужного “ урока превратится в любимый предмет, куда идут с желанием и интересом.
Ведь математика - это нечто большее, чем просто умение работать с цифрами, это основа современной жизни, а потому мы просто обязаны сделать математическое обучение более насыщенным и интересным.








