К другим статьям
Эта статья — авторское мнение колумниста. Мнение автора может не совпадать с мнением редакции «Педсовета».
Хорошо известно, что задачи на применение формулы полной вероятности можно решать не только с помощью этой формулы, но и путём построения дерева вероятностей для рассматриваемого случайного опыта. Данный приём хорошо известен и особенно подходит тем школьникам, у которых «живое», образное мышление превалирует над абстрактным.
Однако с заданиями на формулу Байеса (которая, по сути, всего лишь следствие формулы полной вероятности) дела обстоят совершенно иначе. Подобные задачи не так просто сделать исключительно с помощью вышеупомянутого дерева вероятностей, без применения формул, да и решения, произведённые таким образом, выглядят довольно неуклюже. Уж лучше выполнять эти задания с помощью формул (полной вероятности и Байеса), чем буквально притягивать за уши использование дерева случайного опыта или «прививать» к этому дереву формулу Байеса. Всё равно то, что при этом получается, оказывается непонятным для школьников с превалирующим образным мышлением, а учащиеся-логики справедливо спрашивают: зачем вообще тогда надо тратить время на изображение и заполнение дерева, если можно просто вычислить искомое с помощью формул? Надо быть последовательными, в конце-то концов: или опираться только на формулы, или уж как-то ухитриться применить лишь деревья, вовсе отказавшись от использования каких-либо формул и ограничившись правилами умножения (для вычисления вероятностей произведений событий) и сложения (для расчёта вероятностей «простых» событий).
В данной работе предлагается метод решения подобных задач, отвечающий на эти (вполне разумные, на мой взгляд) претензии и основанный на построении особого дерева вероятностей, которое изображается и заполняется числами на основании исходных данных и элементарных расчётов (последние так или иначе придётся производить для нахождения полной вероятности). Таким образом, кроме изображения второго дерева, иных добавочных действий не понадобится.
Продемонстрируем метод дополнительного дерева на примере решения одного из прототипов задания № 5 профильного ЕГЭ по математике.
Задача
Всем пациентам с подозрением на заболевание делают анализ крови. У больных анализ выявляет болезнь (даёт положительный результат) с вероятностью 0,95; у здоровых – с вероятностью 0,02. Известно, что 6% пациентов, поступивших с подозрением на болезнь, в самом деле больны. Найти вероятность того, что пациент, получивший положительный результат анализа, действительно болен.
Решение
Сформулируем гипотезы: Н1 – «пациент болен», Н2 – «пациент здоров». Событие, полную вероятность которого мы будем вычислять, обозначим А – «анализ дал положительный результат». Нам нужно найти Р (Н1|А).
По условию, Р(Н1) = 0,06; Р(Н2) = 0,94; Р (А|Н1) = 0,95; Р (А|Н2) = 0,02. Все эти данные мы применим при построении и заполнении дерева вероятностей, рядом с ветвями которого укажем соответствующие условные вероятности (см. рис. 1).
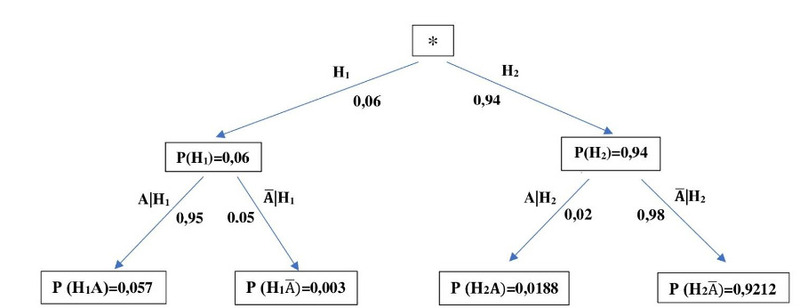
Рис. 1
Найдём Р(А) по данному дереву, просто сложив те вероятности последней строки, при записи которых используется А (а не A): Р(А) = Р (Н1А) + Р (Н2А) = 0,057 + 0,0188 = 0,0758. При классическом подходе далее Р (Н1|А) находится с помощью формулы Байеса.
Мы применим иную методику. Построим и заполним особое дерево вероятностей, которое назовём дополнительным (см. рис. 2). Это тоже дерево вероятностей, которое заполняется с помощью правил сложения (в том числе, для нахождения вероятности противоположного события по вероятности данного события) и умножения. Однако в дополнительном дереве в качестве гипотез будем использовать уже не Н1 и Н2, а А и A (после нахождения Р(А), которое мы произвели выше, уже можно спокойно работать с такими гипотезами, ибо мы теперь знаем их вероятности). Искомую вероятность Р (Н1|А) обозначим х.
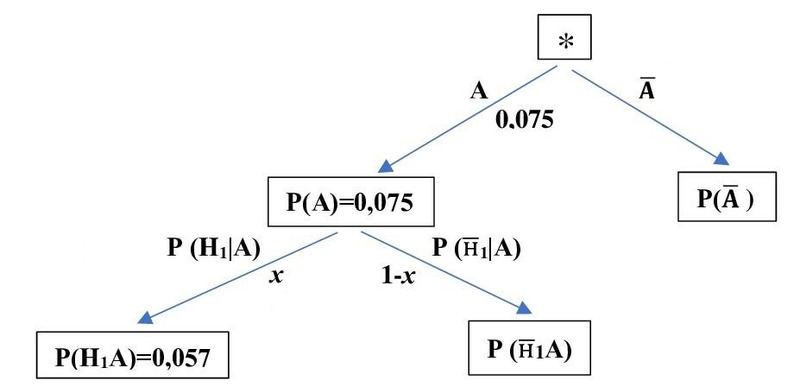
Рис. 2
Найденная нами при заполнении «основного» дерева вероятность Р(Н1А), с одной стороны, составляет 0,057; с другой же стороны, найденная по дополнительному дереву, она равна 0,0758х. Отсюда х = 0,057: 0,0758 = 0,751978… ≈ 0,7520.
Думается, приведённого выше примера вполне достаточно для прояснения сути метода дополнительного дерева. Тем не менее, приведём общий план решения задач на формулу Байеса вышеупомянутым методом.
Прежде всего, хотелось бы отметить, что формулу Байеса необходимо применять в тех случаях, когда в задаче наличествует чётко выделенная полная группа (попарно несовместных) гипотез Нi (отнюдь не обязательно простейшая группа из гипотезы и её отрицания, как в вышеприведённом примере), вероятности которых известны, и рассматривается некоторое событие А, для которого даны его условные вероятности в случаях справедливости каждой из гипотез. Требуется найти вероятность справедливости одной из гипотез (без ограничения общности можно считать, что это гипотеза Н1) при условии, что произошло событие А. Иначе говоря, надо вычислить Р (Н1|А).
Алгоритм работы по методу дополнительного дерева следующий. Вначале (стандартным образом) определяем «полную» вероятность Р(А). Для этого строим основное дерево вероятностей и вычисляем все относящиеся к нему «обычные» и условные вероятности, используя правила произведения и суммы (см. пример). Подробно описывать этот этап не будем, так как всем заинтересованным он хорошо знаком. Затем, складывая вероятности тех событий последнего слоя, которые имеют вид НiА, находим Р (А).
Теперь строим дополнительное дерево. Фактически оно всегда выглядит так, как на рис. 2 (его даже можно ещё упростить, см. замечание чуть ниже). В качестве новых гипотез рассмотрим события А и A. Вероятность первого события мы только что нашли, вероятность второго нам на деле не нужна (хотя легко находится как 1 – Р(А)). Искомую вероятность Р(Н1|А) примем за неизвестную (допустим, х) и заполним дерево, нанеся на него найденные ранее численные значения Р(А) и Р(Н1А), а также х в качестве значения Р(Н1|А). Осталось применить правило умножения для нахождения х: Р(А)∙х = Р(Н1А). причём на практике формальные обозначения в этом равенстве оказываются заменены числами, что облегчает жизнь учащимся с острой идиосинкразией к сложным математическим обозначениям.
Если присмотреться, становится очевидно, что в дополнительном дереве нам фактически нужны всего две ветви: ведущая от корня к вершине первого слоя, обозначенной Р(А), и от этой вершины к вершине второго слоя, обозначенной Р(Н1А). Однако и в «обычном» дереве для решения реально требуются не все ветви, но лишь ведущие к вершинам, в обозначениях которых имеется А (не A). Остальные ветви изображаются из сугубо эстетических соображений. То же имеет место и при использовании дополнительного дерева.
Разумеется, метод дополнительного дерева – не более чем приём, но, хочется надеяться, он будет полезен как коллегам при работе со школьниками, плохо воспринимающими сколько-либо сложные формулы (а подобных учащихся довольно много; более того, по моим наблюдениям, большинство, имея выбор между применением формул либо рисованием дерева, выбирают последнее), так и самим этим школьникам при решении заданий на формулу Байеса. Фактически мы можем изобразить лишь основное и дополнительное деревья, нанести на нужные ветви и вершины числа, используя лишь простые и легко усваиваемые правила умножения и сложения – и найти х. При этом сложные обозначения, типа Р(Н1А) и Р(Н1|А), можно вовсе не применять. Итого: визуализация и два элементарных правила позволяют обучить большинство школьников решать задачу, которая при стандартном подходе представляет для них значительные трудности.
Метод дополнительного дерева прост в освоении и использовании и, возможно, поможет многим учащимся преодолеть психологический и интеллектуальный барьер, мешающий им выполнять задания на формулу Байеса.
Материалы по теме:
- Можно ли заинтересовать ребёнка математикой с помощью олимпиад?
- Как избежать математической травмы у ученика
- 7 игр для развития математических способностей у детей
Иллюстрация: Александр Митин
